Algorithm Design Book - Chapter 6
Hashing and Randomized Algorithms
Balls and Bins
Hashing can be seen as assigning bucket for a given ball(or value). If we get lucky, we will always have a single ball in each bucket. This ensure we have an expected access time of O(1). Some of the probability related jargon involved has been mentioned in the book.
Randomization In Hashing
In hashing we saw that things can go really wrong for some inputs. To prevent that we add some randomization to the hashing function. This makes sure that worst case in hashing is not attached to a particular input. Rather it is due to really bad luck.
So Instead of using simple hashing i.e. \(h(x) = f(x)mod(m)\) we add a random number \(p(f(x) >> p >>m)\), which provides randomization to our hashing function. \(h(x) = (f(x)mod(p))mod(m)\)
Bloom Filters
What’s this about? To prevent multiple false positives, we can use this technique to reduce the probability of false positives. In normal hashing, we calculate h(x) and check if the value stored is same as the searched input.
Instead of that we can have multiple hashing functions \(h_1(x), h_2(x), ..., h_k(x)\). When we search for a value, we calculate all these hashes and check if we get a set bit for each of these hash functions.
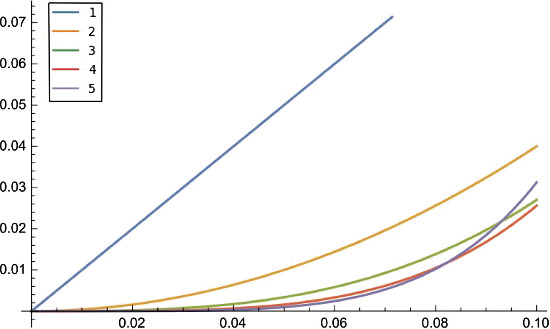
We can see that for \(k >= 2\), we get reduced probabilities
Minwise Hashing
This is one of the new things, I learnt from this book. It is mostly using probability to make some conclusions which are useful.
Minwise hashing is a clever but simple idea to do this. We compute the hash code \(h(w_i)\) of every word in \(D_1\), and select the code with smallest value among all the hash codes. Then we do the same thing with the words in \(D_2\), using the same hash function.
What is cool about this is that it gives a way to pick the same random word in both documents. Suppose the vocabularies of each document were identical. Then the word with minimum hash code will be the same in both \(D_1\) and \(D_2\), and we get a match. In contrast, suppose we had picked completely random words from each document. Then the probability of picking the same word would be only \(1/v\), where \(v\) is the vocabulary size.
It can also be useful to get the number of distinct values in a stream in constant time. It won’t give the exact value but it can be used to get an estimate of the number of distinct values. It can be calculated using the below expr. For proof, you can go through the book. No. of distinct values = \(O(M/Minwise Hash)\)
Here M is the size of the output space of the hashing function.